La paradoja de St. Petersburg, es un juego teórico usado en economía para representar un ejemplo clásico donde, teniendo en cuenta solamente el valor esperado como el único criterio de decisión, el encargado de la toma de decisiones estará equivocado y tomará una decisión irracional. Esta paradoja fue presentada y resuelta en «Commentarii Academiae Scientiarum Imperialis Petropolitanae» de Daniel Bernoulli (traducido como «Exposición de una nueva teoría en la medición de riesgo»), publicado en 1738. Bernoulli solucionó la paradoja haciendo la distinción entre valor esperado y utilidad esperada, ya que esta última utiliza la utilidad multiplicada por las probabilidades, en lugar de utilizar los resultados ponderados. Sin embargo, desde entonces, se han utilizado enfoques alternativos por diversas investigaciones para responder a esta paradoja.
La clave de la paradoja es determinar el valor que alguien estaría dispuesto a pagar para jugar a un juego de lotería que funciona así: una moneda es lanzada, y si la cara aparece, al jugador se le paga $2 (el monto pagado para jugar es $1); si sale cruz, la moneda se lanza otra vez, hasta que la cara aparezca, duplicando la ganancia inicial cada vez que la moneda se lanza. Por ejemplo, para el sorteo número 3 (n = 3), el beneficio sería 8 (2n) y el valor esperado, que aquí equivale a la recompensa multiplicada por la probabilidad (aquí, 1).
La probabilidad de que la primera cola aparezca en el lanzamiento número n es igual a pn = 1/2n, siendo 2n el beneficio. Por lo tanto, el valor esperado de n lanzamientos sería:
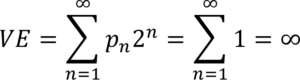
Si usamos el valor esperado como criterio de decisión, el jugador debería estar dispuesto a pagar $∞ para jugar. Sin embargo, ningún individuo racional aceptaría esto. Para Bernoulli, la respuesta se basó en el uso de la máxima utilidad esperada en lugar del máximo valor esperado:
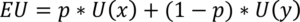
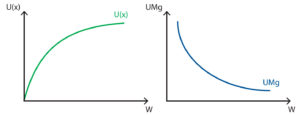
Por otra parte, Bernoulli indicó que la utilidad se incrementará con la riqueza del jugador (ya que él o ella tendría más dinero para jugar) y disminuirá la utilidad marginal.
La probabilidad de que la primera cola aparezca en el lanzamiento número n es igual a pn = 1/2n, siendo 2n el beneficio. Por lo tanto, el valor esperado de n lanzamientos sería:
Si usamos el valor esperado como criterio de decisión, el jugador debería estar dispuesto a pagar $∞ para jugar. Sin embargo, ningún individuo racional aceptaría esto. Para Bernoulli, la respuesta se basó en el uso de la máxima utilidad esperada en lugar del máximo valor esperado:
Por otra parte, Bernoulli indicó que la utilidad se incrementará con la riqueza del jugador (ya que él o ella tendría más dinero para jugar) y disminuirá la utilidad marginal.




