Tipos de discontinuidades de una función en un punto

1. Discontinuidad evitable
En este caso no se cumple la condición (a) de la definición de continuidad, es decir existe el límite finito L de f(x) en x = a pero f(x) no está definida en a. La función puede modificarse adoptando como f(a) el valor L correspondiente, convirtiéndose así en una función continua en x = a.

También se clasifica como evitable la discontinuidad en la que no se cumple la condición (c) de la definición de continuidad, es decir, existen f(a) y 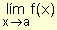, pero no coinciden. En este caso, puede salvarse la discontinuidad tomando como valor de la función el resultado del límite.

2. Discontinuidad de primera especie

a) Discontinuidad de salto

Existen los límites laterales pero son distintos.

 b) Discontinuidad infinita

Al menos uno de los límites laterales no existe.

3. Discontinuidad de segunda especie

Una discontinuidad es esencial o de segunda especie si no existe alguno de los límites laterales en x = a.

Ejemplo. Dadas las siguientes gráficas de funciones, indique el tipo de discontinuidad en cada caso.

1)	2)
3)	4)

1) El límite de y = f(x) para x tendiendo a 5 existe y es 4, pero 5 no pertenece al dominio de la función. Se trata de un discontinuidad evitable en x = 5.

2) En x = 2 hay una discontinuidad esencial porque no tiene límite por la derecha.
3) Observando la gráfica se deduce que y . Como los límites laterales existen pero son distintos es una discontinuidad de salto.

4) Los límites laterales no existen pues y . La función presenta una discontinuidad infinita en x = 5.